Когда в году 360 дней - Блог Р7-Офис

Почему все месяцы разные по длительности, это же неудобно! Примерно так рассуждали некоторые европейские специалисты в области права и финансов, которые 50 лет назад договорились, что в некоторых случаях год равен 360 дням, а каждый месяц – 30. А когда появились редакторы электронных таблиц, на этот случай предусмотрели функцию ДНЕЙ360.

Варианты применения функции ДНЕЙ360 в быту придумать сложно, зато она официально используется как минимум при расчете различных процентов: за пользование чужими денежными средствами, начисление по облигациям внутреннего госзайма и других.

Наряду с экзотикой поговорим про более понятную функцию ДНИ, вместе с которой они входят в группу функции даты и времени.

ДНИ и ДНЕЙ360

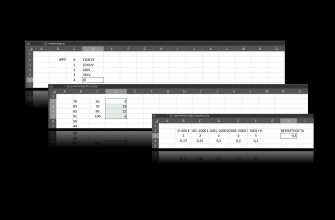
Проиллюстрируем различие между функциями ДНИ и ДНЕЙ360 на простом примере, который отображен ниже на снимке экрана. У нас есть даты начала и конца некоего периода. В строке 3 они фиксированы, в строке 4 дата окончания задана функцией СЕГОДНЯ() – она очень простая, даже аргумента нет, только пустая скобка.

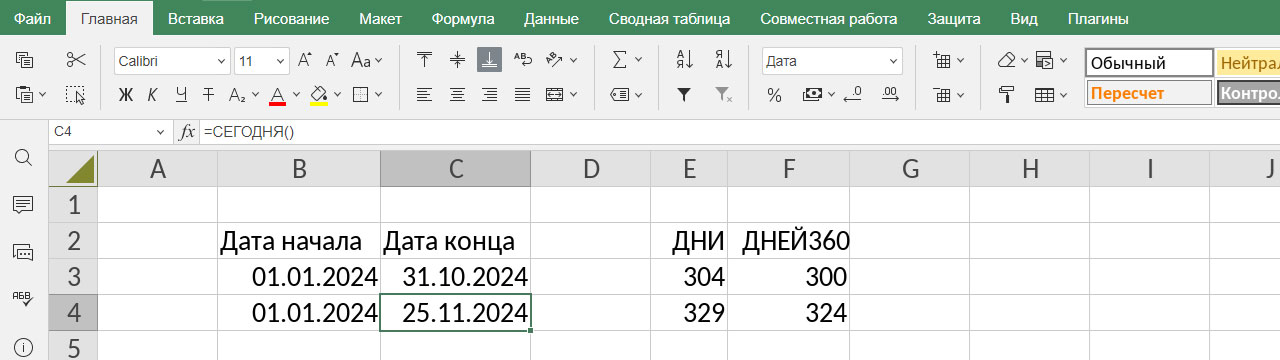
В столбцах E и F вы видите количество дней, которое подсчитали две функции: ДНИ – из расчёта 365 дней в году, ДНЕЙ360 – исходя из условного круглого года.

Посмотрим на синтаксис: =ДНИ(кон_дата; нач_дата). Всё просто, но обратите внимание, что сначала указан последний день. Кстати, СЕГОДНЯ() можно вставить прямо в формулу. Если вы перепутаете начало и конец, то сразу это увидите, поскольку значение станет отрицательным.

В случае ДНЕЙ360 мы опять имеем два обязательных аргумента плюс появляется необязательный:

=ДНЕЙ360(нач_дата; кон_дата; [метод])

Обратите внимание, что даты начала и конца поменялись местами по сравнению с функцией ДНИ. Не спрашивайте, почему так случилось, мы не знаем ответа.

Аргумент метод – это логическое значение ИСТИНА или ЛОЖЬ. В первом случае вычисление выполняется с помощью европейского метода, согласно которому начальная и конечная даты, которые приходятся на 31-й день месяца, полагаются равными 30-му дню того же месяца.

Если этот аргумент имеет значение ЛОЖЬ или отсутствует, вычисление выполняется с помощью американского метода, согласно которому, если начальная дата является последним днем месяца, она полагается равной 30-му дню того же месяца. Если конечная дата является последним днем месяца, а начальная дата меньше, чем 30-е число, то конечная дата полагается равной первому дню следующего месяца.

Пример использования

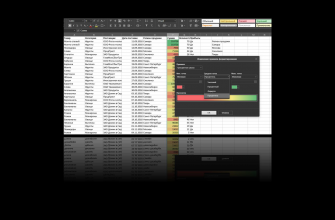
Давайте посчитаем сумму, которая накапливается на депозите с ежедневной капитализацией. Даны первоначальный взнос, дата открытия и ставка. Для расчета используется формула S=P*(1+%/N)*T, где P – начальный взнос, N – число дней в году, T – число дней от взноса до текущего момента. Данные представлены на снимке экрана. Для расчёта нам нужны две формулы:

=C7*(1+(C8/365)*ДНИ(СЕГОДНЯ();C9))
=C7*(1+(C8/360)*ДНЕЙ360(C9;СЕГОДНЯ()))

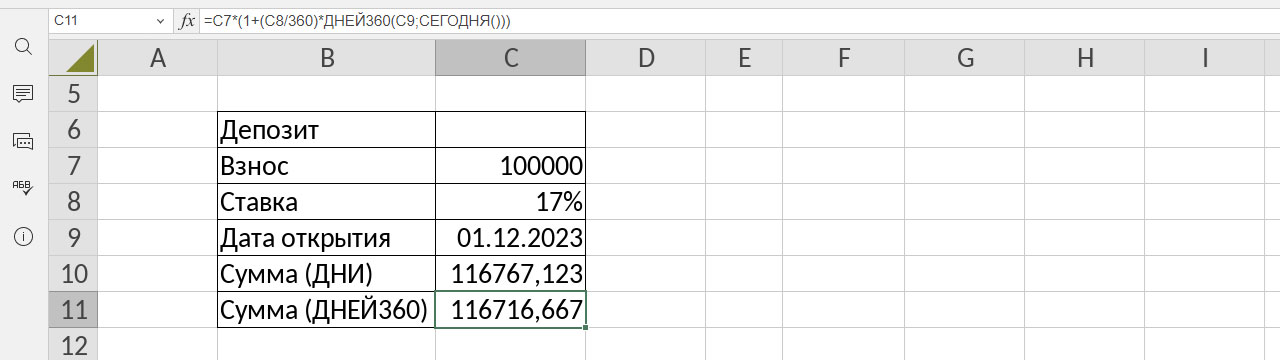
Как видно, разница невелика, но она есть, а в мире финансово всё должно быть по правилам. Это в нашем примере показания отличаются на условные 50 рублей. А если там 50 млн? Вы можете ожидать прибавки, рассчитанной исходя из 365 дней, а банк по умолчанию берет за основу 360. И это скорее всего даже где-то пропечатано мелким шрифтом, но не все же этот текст читают. Поэтому – уточняйте правила и пользуйтесь правильной формулой.

А если вы решаете с помощью редактора электронных таблиц другие задачи, посмотрите другие посты по теме:

Если вы хотите получить больше информации, то можете воспользоваться рубрикатором и поиском, которые расположены справа от этого текста, посмотреть популярные и похожие статьи. Помимо этого у нас на сайте есть база знаний в карточках, а еще много увлекательного контента в VK и в Te l egram. Там же есть возможность написать нам, поделиться своим опытом и задать вопросы. А еще вы можете задавать свои вопросы нашему боту Лёлику и сразу получать ответы. Попробуйте сами!